如何一口气理解PageRank
一口气开始别憋气
终于 Tex 调好了 刚好最近又多次提及 PageRank 于是~
目测这一系列 有个两三篇 blog
PageRank 是 由佩奇(Larry Page)等人提出 的 Google 最为有名的技术之一
我 乔治 甘拜下风
PageRank 是一种基于随机游走 的 评价网站权值的算法
言而总之 PageRank 是一种十分重要的算法 不管在学术界 还是在产业界
Node Similarity & Proximity
在介绍 PageRank 需要先来提一下 什么叫节点相似
假设在一个有向图集合 G(V, E)中研究两个节点 u, v 之间的相关性
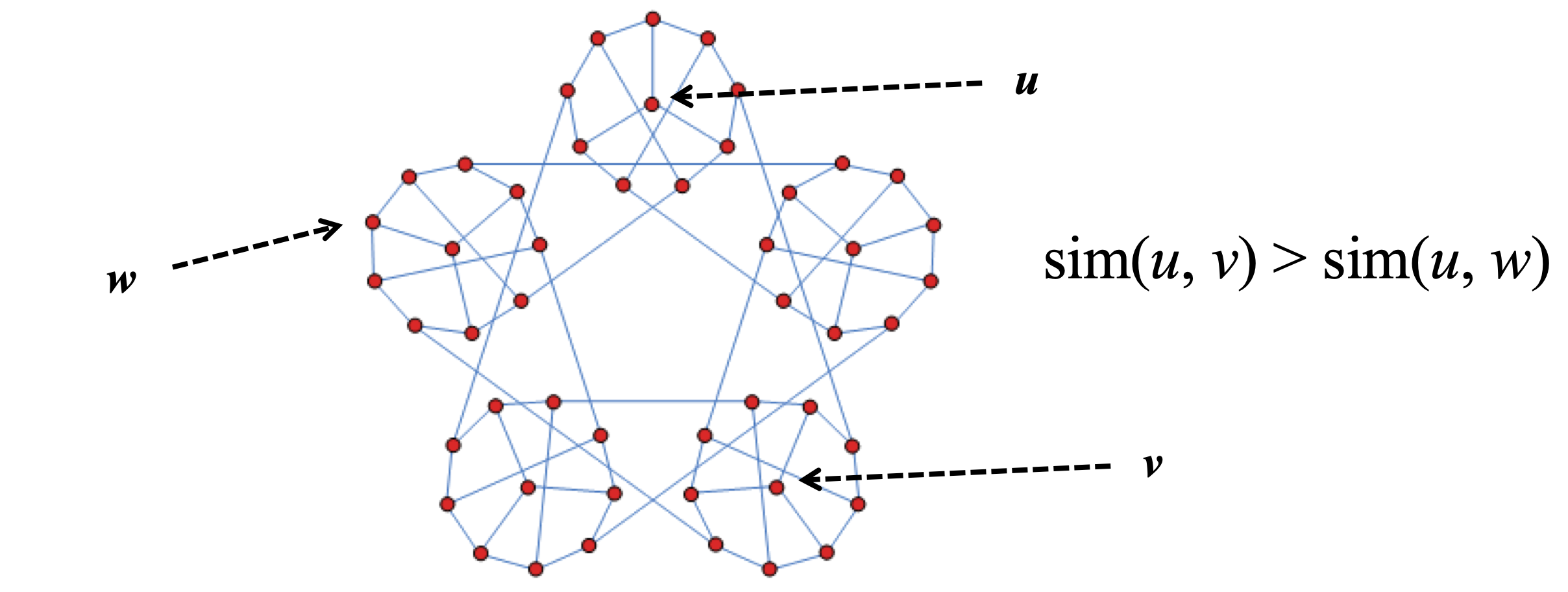
上图, 我们可以从感性的认识上判断 u, v 之间的相似高要比 u, w 之间的相似度要高
那如何来具体定义相似度呢
Common neighbor
我们很容易可以想到 好像 一个节点的邻居集合可以表征这个节点的周围结构
实际上这就是 CN 算法(common neighbor)
规定\begin{equation}CN(u, v)=nei(u)\cap nei(v)\end{equation}
Jaccard
单纯的数值对于估计一个节点的相似度 可能存在标准不统一的情况
故 jaccard 在 CN 的基础上做了一个归一化的处理
得到\begin{equation}Jaccard=\dfrac{CN(u, v)}{nei(u)\cup nei(v)}\end{equation}
Adamic-Adar Index
\begin{equation}Adamic-Adar Index=\sum \dfrac{1}{logN(v)}\end{equation}
当然还可以按计算时用到部分点还是全部点来进行分类
local- Common Neighbors(CN), Jaccard, Adamic-Adar Index
grobal- Personalized PageRank(PPR), SimRank, Katz
事实上 节点相似度在生产过程中有极强的落地场景
尤其是和社交网络分析相关的好友推荐
另外 还可以运用在 Top-k 的关系发现当中
传言王者荣耀的好友推荐 就是用 PPR 做的
最后需要提一句 $Node Similarity\not = Node Proximity$
一般而言, $sim(u, v) = sim(v, u)$, 但$p(u, v) \neq p(v, u)$
Naive PageRank
\begin{equation}PR(u)=\sum\limits_{v \in N_{in}(u)}^N \dfrac{1}{N_{out}(v)}PR(v)\end{equation}
S.t.$PR(u) \ge 0$, $\sum PR = 1$
直观上看 PR 值的计算是一个迭代的过程,通过出度把 PR 值分配给下游节点
但 Naive PageRank 在计算的过程中会出现一些问题
$\vec {PR} = P^T \cdot\vec{PR}$,其中$P$为行向量
故$\vec {PR}^T = \vec{PR} ^T \cdot P$
因为上述 PageRank 的定义是一个递归过程,所以需要一个递归停止条件-Error
\begin{equation}max|\vec {PR}^{(l+1)}(i) - \vec {PR}^{(l)}(i)|\le \epsilon\end{equation}
其实严格上还需要证明上述递推关系的收敛性 , 事实上 Naive PageRank 是不一定收敛的
当然还有解的存在性,唯一性 等等
Flaw 1 Multiple Solutions
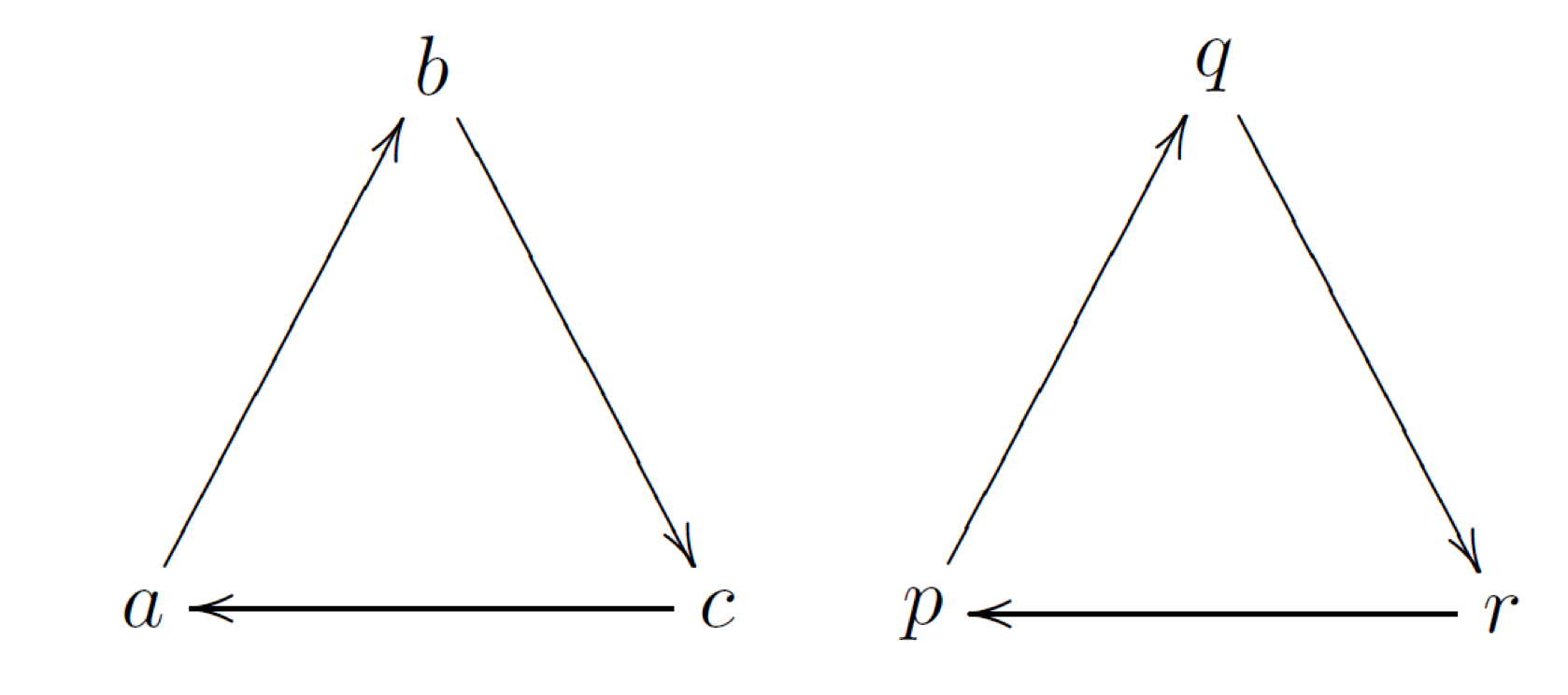
对于图示这种情况 PR 的值其实有无数钟取法
只要满足$PR_a = PR_b = PR_c, PR_p = PR_q = PR_r$
Flaw 2 Link Spam
还是上面的例子 a, b, c 此时$PR_a = PR_b = PR_c = \dfrac{1}{3}$
如果把$c->a$的边改为$c->b$, 迭代后就会造成 $PR_a = 0, PR_b = PR_c = \dfrac{1}{2}$
当一个平衡建立之后,如果因为少数几个节点的异常更改,就会造成全部 PR 值的改变,这就很容易导致少数几个节点操控整个系统的 PR 值
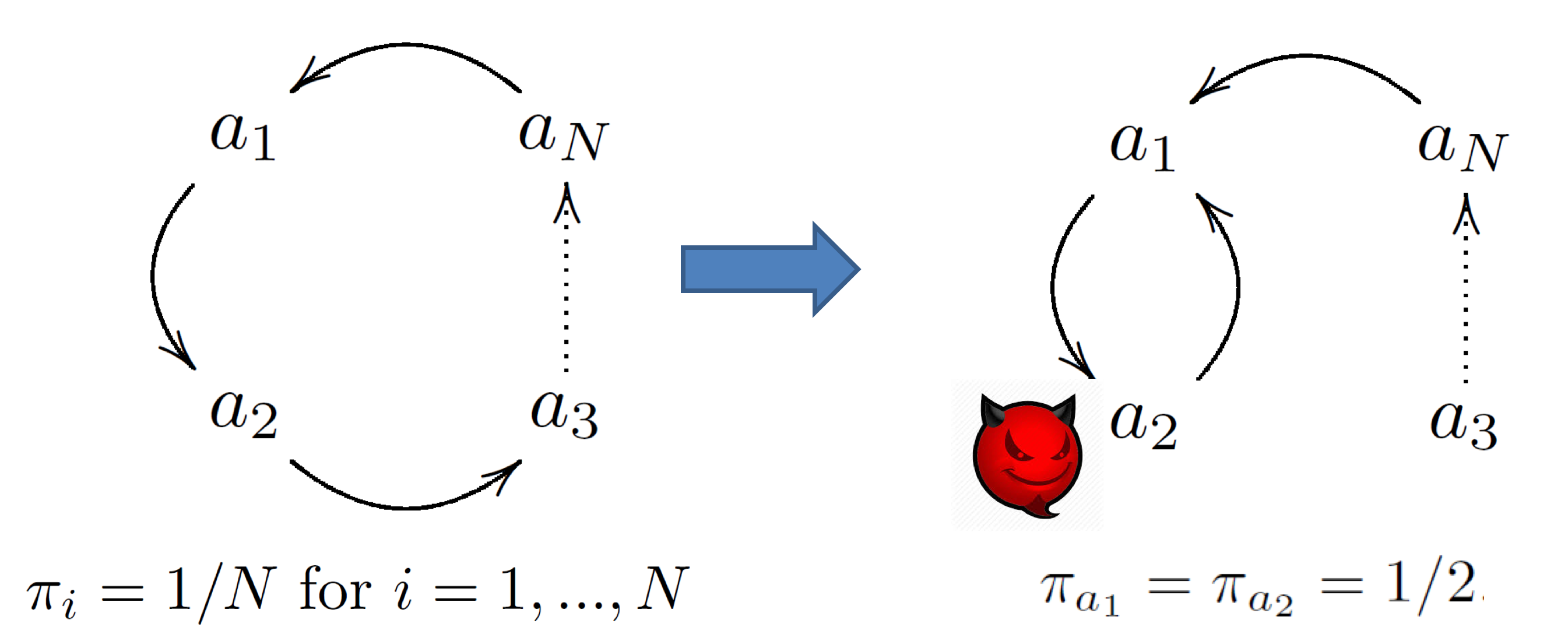
Flaw 3 Dead Ends and Spider Traps
其实仔细想一想 Flaw2 是因为其他节点变得没有入度造成的
那么如果有那么一些点是只入不出的,则会造成 PR 值随着迭代向该点聚集
这样的点 可以看做 强连通子图
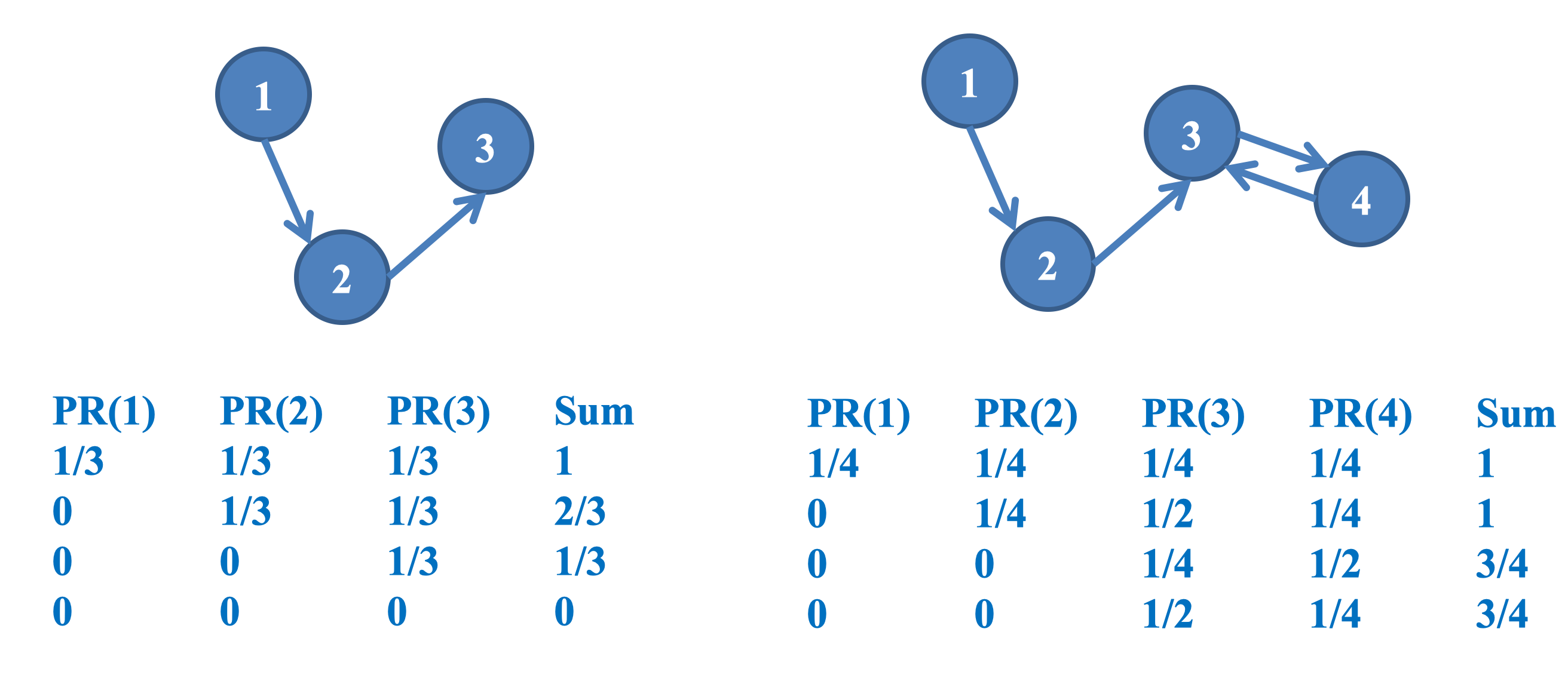
PageRank
为解决上述的问题 佩奇 提出
\begin{equation}PR(u)=\alpha \sum\limits_{v\in N_{in}(u)}^N \dfrac{1}{N_{out}(v)}PR(v)+ (1-\alpha)\dfrac{1}{n}\end{equation}
相对于 Naive PageRank 相对于做了一个平滑处理 给一个偏置量
- Flaw 1.
$PR(a) = PR(b) = PR(c) = PR(p) = PR(q) = PR(r) = \dfrac{1}{6}$ - Flaw 2. 减少出现 Link Spam 的可能性
- Flaw 3. Doesn’t help ☹
- 移除没有出度的节点或者结构
- 加一条回边
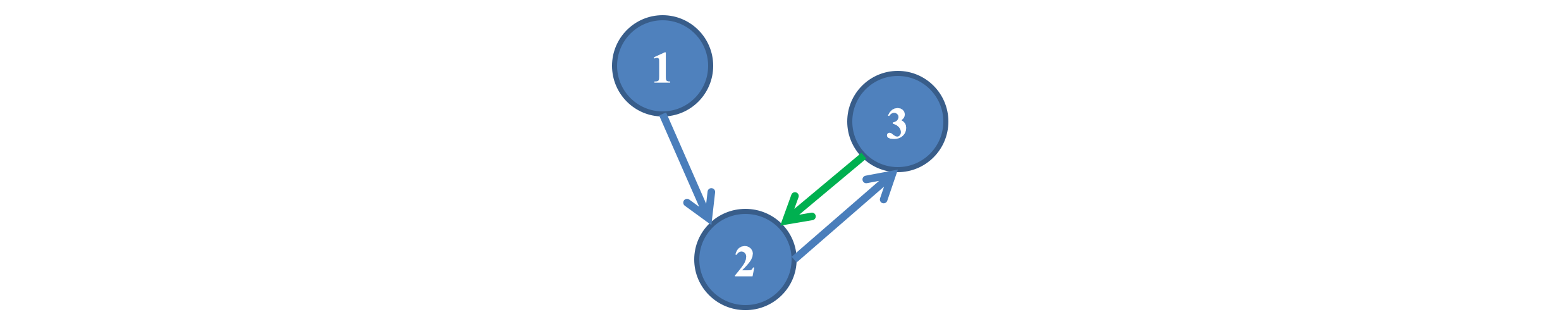
正如前面所说的,因为 PageRank define by 递归
所以,我们需要证明解的存在性,唯一性,收敛性,此处省略若干证明
收敛性: 我们用矩阵形式表示$\pi = \vec {PR}$
则根据上述定义可得,
\begin{equation}\pi_v^{(t)}= (1-\epsilon)\sum\limits_{(w,v) \in E} \dfrac{\pi_w^{(t-1)}}{d_w}+\dfrac{\epsilon}{n}\end{equation}
则\begin{equation}Err(t)=\sum\limits_v|\pi_v^{(t)}-\pi_v^*|\end{equation}
而\begin{equation}|\pi_v^{(t)}-\pi_v^*| \le (1-\epsilon)\sum\limits_{(w,v) \in E} \dfrac{\pi_w^{(t-1)} - \pi_w^*}{d_w}\end{equation}
则\begin{equation}Err(t)=\sum\limits_v|\pi_v^{(t)}-\pi_v^*|\le (1-\epsilon)\sum\limits_w [\pi_w^{(t-1)} - \pi_w^* ]\le(1-\epsilon)Err(t-1)\le(1-\epsilon)^tErr(0)\end{equation}
当$0<\epsilon <1$时,上述递推关系式具有收敛性
把第 t 轮递推式子依次带入 t-1, t-2, ...
得到\begin{equation}\vec{PR}^{l \cdot T}=\alpha ^l\vec{PR}^{0\cdot T}P^l+\dfrac{1-\alpha}{n}\vec{1}^T(\alpha^{l-1}\cdot P^{l-1}+\cdot \cdot \cdot+\alpha P + I)\end{equation}
可以看出当迭代轮数 l 比较大时,$\alpha ^l$会是一个小量,造成 PR 只剩下第二项
故\begin{equation}\vec{PR_v}^T=\dfrac{1-\alpha}{n}\vec{1}^T(\alpha^{l-1}\cdot P^{l-1}+\cdot \cdot \cdot+\alpha P + I)\end{equation}
对于这个式子的含义学术界有很多解释
$Random-Walk$: 看作是以概率$\alpha$留下,$1-\alpha$转移随机游走的概率值$PR(v)$= # walks ends at$\dfrac{v}{nr}$
- 看做是一个长时间随机游走的结果
$\alpha-Walk$: 与 Random Walk 一致, 看做是一个以概率$\alpha$留下,$1-\alpha$转移随机游走过程,约定经过某个点,该点的$score(w) +=(1-\alpha)$$\alpha-Walk$相对于 Random Walk,方差更小,复杂度很低,实际效果更好,是目前研究的热点方向
Next maybe Talk About PPR/SimRank or maybe Top-k PPR
好 一口气结束 hhh