试谈RNN中门的变迁
终于发完 proposal 的邮件 深吸一口气
希望明天不要被怼的太惨
已经连续 高强度(hua shui) 看 paper n 天了
一切 索然无味
随着看到的 paper 层次越来越高
就越发羡慕搞NLP的
昨天还在跟室友说 一开始觉得写SMN的WuWei dalao 指不定是个中年油腻大叔
结果人家研究生还没毕业
哇 满脸的羡慕
言归正传 打算用两三篇 blog 讲一下最近学习的多轮检索式对话这个领域
第一篇就来谈一谈 在检索式对话中用到最多的 RNN 模型家族 (之所以 称之为 家族 因为变种太多了)
Naïve RNN
RNN = Recureent Neural Network
翻译成中文就是循环神经网络(注意不是递归,虽然它的过程很递归)
和传统的卷积神经网络CNN 全连接神经网络DNN不同的是其包含时序信息
顺带说一下另外两者的特点
DNN: n 层与 n-1 层每个都有关, 参数数量级巨大;
CNN: 卷积+pool,至于什么是卷积?加权叠加
这一点十分有利于用于训练和时间相关的 Dataset 尤其是 NLP 方面
有没有觉得很像马尔科夫链(en 不是过程 就是链)
事实上在有 CNN 之前 确实一般都做成隐马尔科夫链
NN 起源于多层感知机 MLP
感知机之所以能战胜同时期的元胞自动机异军突起 主要是其拥有反向传播算法
但 NN 随着训练层数的增大 会出现梯度消失现象 但层度深 确实效果好呀
于是就有一堆学者提出了 各种办法 使得 NN 的层数能够扩展
比如说预处理 高速公路网络(highway network)和深度残差学习(deep residual learning)
时序 不仅仅是 训练结果和之前的转态有关 还是得输出结果长度可变的效果 这点和其他 NN 尤为不同
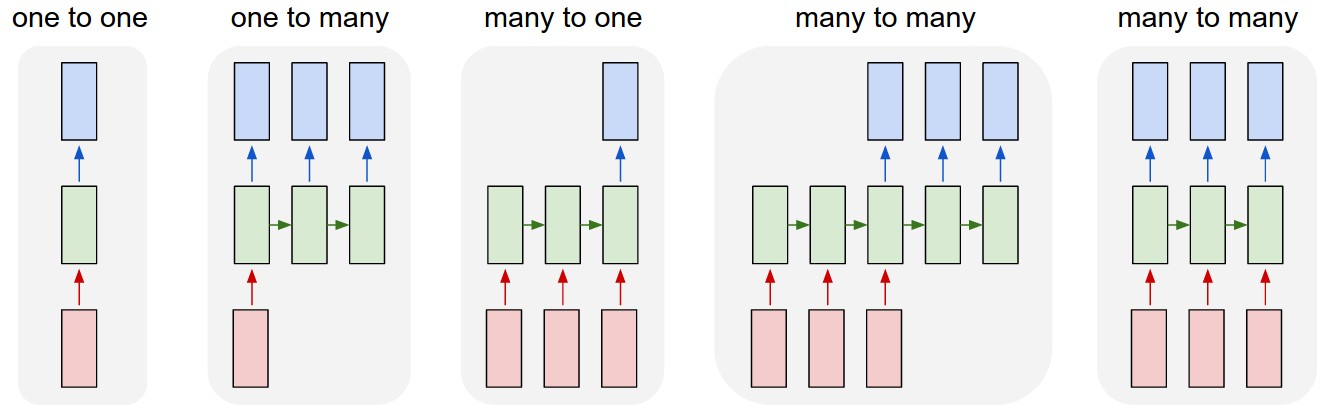
CNN 可以在下一个时间点 把输出作用在节点自身
如果按时间展开 就变成那张经典的图 作用在$t+1$时刻输出$o(t+1)$是该时刻输入和所有历史共同作用的结果
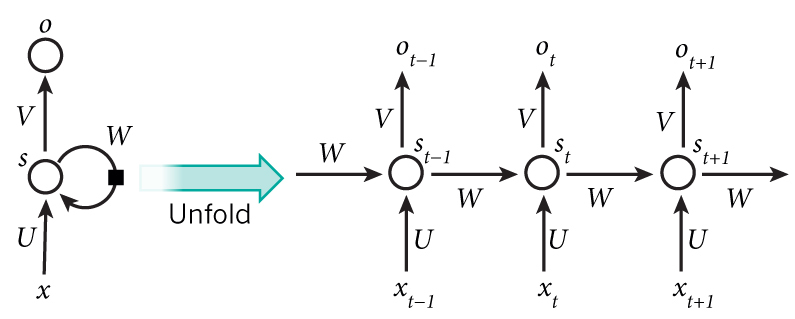
可以看出$s_{t+1}, o_t = f(s_t, x_t, U, V, W)$
和别的 NN 不同的是 RNN 所有步骤共享相同的参数$U, V, W$
有正向的 RNN 很容易想到是不是还有双向的(Bidirectional RNN) 深度(Deep Bidirectional RNN)
但对于上述 RNN 都不可避免的会出现前面说的梯度消失的现象
只不过在这里对的是时间维度上的消失(即 时序信息传播不过 k 间隔)
所以就有了一系列改进版 RNN
LSTM
比如说最著名的LSTM[4]
LSTM = LONG SHORT-TERM MEMORY
其通过门的设置来实现长时期的记忆能力
LSTM 每个时刻的 hidden state 包含了多个 memory blocks
每个block包含了多个 memory cell
每个 memory cell包含一个 Cell 和三个门Gate: 输入门,输出门,遗忘门
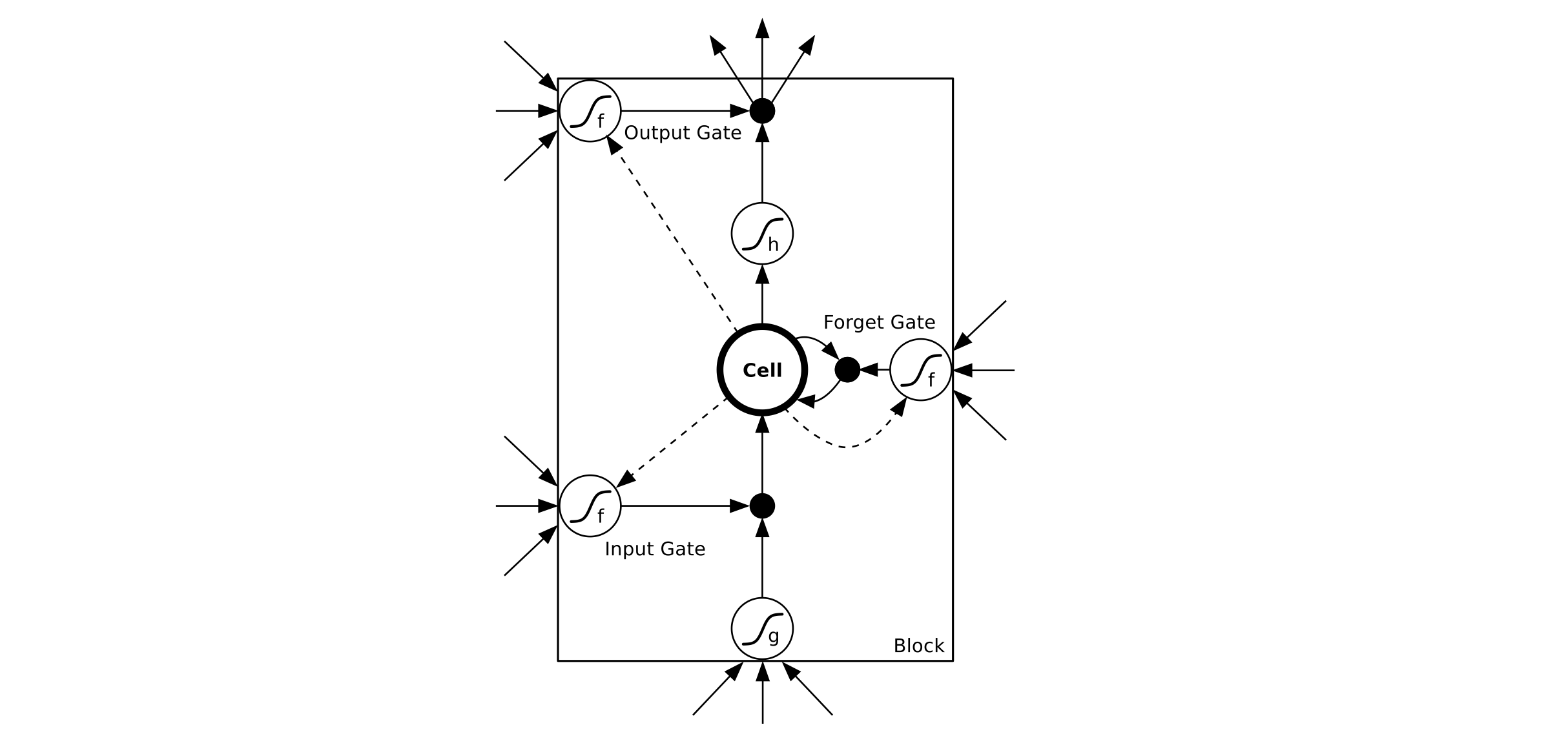
Forward Pass
Input Gate
\begin{equation}a_l^t=\sum\limits_{i=1}^Iw_{il}x_i^t+\sum\limits_{h=1}^Hw_{hl}b_h^{t-1}+\sum\limits_{c=1}^Cw_{cl}s_c^{t-1}\end{equation}
\begin{equation}b_l^t=f(a_l^t)\end{equation}
Forget Gate
\begin{equation}a_\phi^t=\sum\limits_{i=1}^Iw_{i\phi}x_i^t+\sum\limits_{h=1}^Hw_{h\phi}b_h^{t-1}+\sum\limits_{c=1}^Cw_{c\phi}s_c^{t-1}\end{equation}
\begin{equation}b_\phi^t=f(a_\phi^t)\end{equation}
Cell
\begin{equation}a_c^t=\sum\limits_{i=1}^Iw_{ic}x_i^t+\sum\limits_{h=1}^Hw_{hc}b_h^{t-1}\end{equation}
\begin{equation}s_c^t=b_\phi ^ts_c^{t-1}+b_l^tg(a_c^t)\end{equation}
Output Gate
\begin{equation}a_\omega^t=\sum\limits_{i=1}^Iw_{i\omega}x_i^t+\sum\limits_{h=1}^Hw_{h\omega}b_h^{t-1}+\sum\limits_{c=1}^Cw_{c\omega}s_c^t\end{equation}
\begin{equation}b_\omega^t=f(a_\omega^t)\end{equation}
Cell Outputs
\begin{equation}b_c^t=b_\omega^th(s_c^t)\end{equation}
注意 OutPut Gate 中最后一项是$s_c^t$, 而不是$s_c^{t-1}$ 因为此时 Cell 结果已经产生了
Backward Pass
定义 $\epsilon_c^t=\dfrac{\partial \Gamma}{\partial b_c^t}$,$\epsilon_s^t=\dfrac{\partial \Gamma}{\partial s_c^t}$
Cell Outputs
\begin{equation}\epsilon_c^t=\sum\limits_{k=1}^Kw_{ck}\delta_k^t+\sum\limits_{g=1}^Gw_{cg}\delta_g^{t+1}\end{equation}
Output Gates
\begin{equation}\epsilon_\omega^t=f'(a_\omega^t)\sum\limits_{c=1}^Ch(s_{c}^t)\epsilon_c^t\end{equation}
State
\begin{equation}\epsilon_s^t=b_w^th'(s_c^t)+b_\phi^{t+1}\epsilon_s^{t+1}+w_{c\phi}\delta_\phi^{t+1}+w_{cw}\delta_w^t\end{equation}
Cell
\begin{equation}\delta_c^t=b_l^tg'(a_c^t)\epsilon_s^{t}\end{equation}
Forget Gates
\begin{equation}\epsilon_\phi^t=f'(a_\phi^t)\sum\limits_{c=1}^Cs_{c}^{t-1}\epsilon_s^t\end{equation}
Input Gates
\begin{equation}\epsilon_l^t=f'(a_l^t)\sum\limits_{c=1}^Cg(a_{c}^{t})\epsilon_s^t\end{equation}
可以看出 Forget Gates 和其他两个 Gates 在指数上略有差别
嗯 我放这么些公式就是想要恶心大家的
我已经料想到没什么人 可以看到这里了
实际上你可以把 LSTM 想象成一个传送带,从过去一直拉到未来
而门则是管控上下这根传送带尽职的保安大叔
Forget Gate 规定着什么时候必须下车放心 这是去幼儿园的车
Input Gate 负责到点把东西放入传送带
Output Gate 负责到点把东西从传送带输出(Forget 是无用的 Output 是有用的)
结合下图再理解下
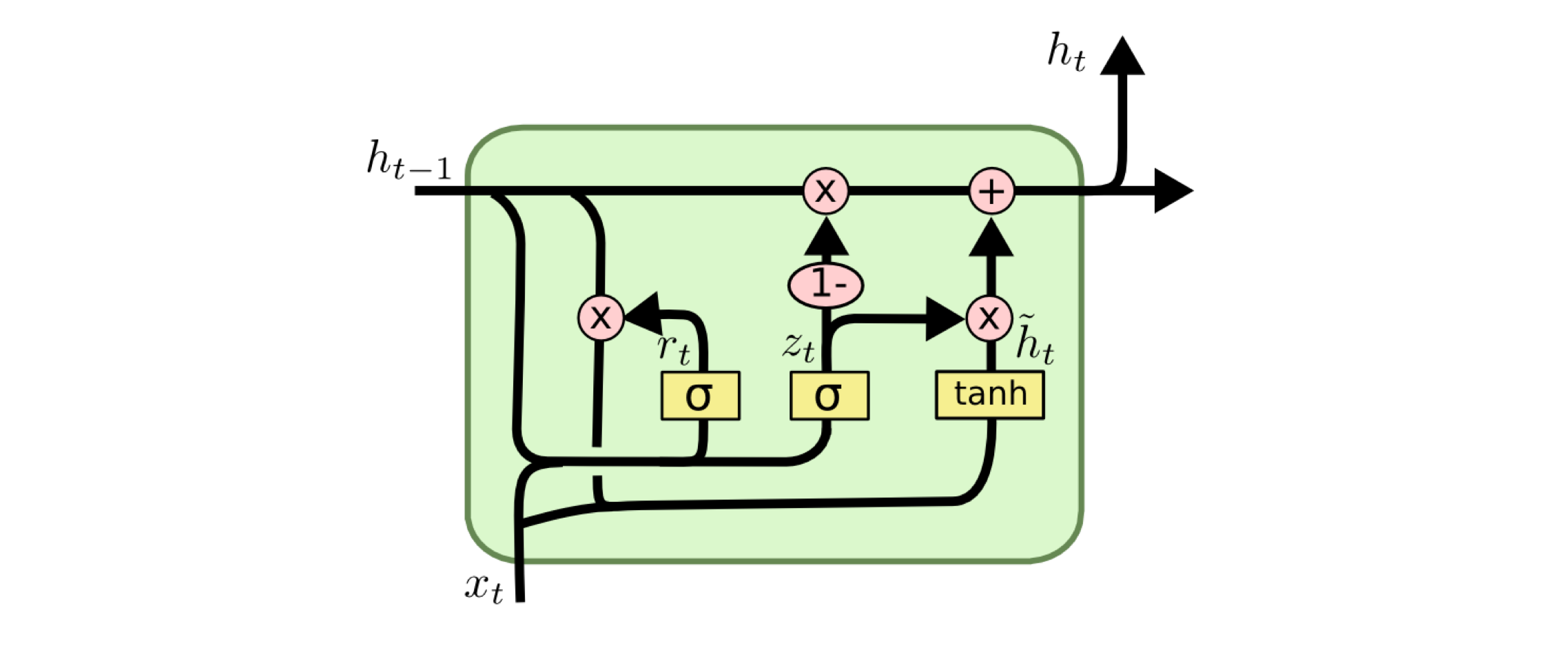
GRU
注意到 LSTM 有三个门
在计算时这三个门都需要进行迭代 在计算时耗时较大 并行操作空间较小
故提出了GRU 模型[9]
其通过Update Gates 替代Output Gates + Forget Gates
把Cell State 和 隐状态$h_i$ 合并
- LSTM 转态转移方程(这才是需要记得公式)
\begin{equation}i_t=\sigma(W_is_{t-1}+U_ix_t+b_i)\end{equation}
\begin{equation}o_t=\sigma(W_os_{t-1}+U_ox_t+b_o)\end{equation}
\begin{equation}f_t=\sigma(W_fs_{t-1}+U_fx_t+b_f)\end{equation}
\begin{equation}\tilde{s_t}=\phi(W(o_t\bigodot s_{t-1}))+Ux_t+b)\end{equation}
\begin{equation}s_t=f_t\bigodot s_{t-1}+i_t\bigodot \tilde{s_t}\end{equation}
其中 i, o, f 分别代表 input, output, forget gates
- GRU 转态转移方程
\begin{equation}r_t=\sigma(W_rs_{t-1}+U_rx_t+b_r)\end{equation}
\begin{equation}z_t=\sigma(W_zs_{t-1}+U_zx_t+b_z)\end{equation}
\begin{equation}\tilde{s_t}=\phi(W(r_t\bigodot s_{t-1}))+Ux_t+b)\end{equation}
\begin{equation}s_t=z_t\bigodot s_{t-1}+(1-z_t)\bigodot \tilde{s_t}\end{equation}
其中 r, z 分别代表 reset, update
可以看出转态转移方程少了一个 计算量 势必会下降
很显然 GRU LSTM 也都有对应的双向版本
SRU 及 类似模型
GRU 的结果实际上已经比较好了
但 计算代价还是太大
于是在 16 年末到 17 年 逐渐由学者提出进一步缩减门运算的模型结构
门减少 势必会减小运算量 但之所以引入门 是因为 我们需要更好的传递性
当然在顶会上 发 Paper 的这几个模型 在实际效果上 都不错
我这里写 SRU 不太恰当 Quasi-RNN, MRU都是类似的思想 这里以 SRU 为例来进行分析
直接来看
\begin{equation}\tilde{s_t}=Ws_t\end{equation}
\begin{equation}f_t=\sigma(W_fs_t+b_f)\end{equation}
\begin{equation}r_t=\sigma(W_rs_t+b_r)\end{equation}
\begin{equation}\tilde{s_t}=\phi(W(r_t\bigodot s_{t-1}))+Ux_t+b)\end{equation}
\begin{equation}c_t=f_t\bigodot c_{t-1}+(1-f_t)\bigodot \tilde{s_t}\end{equation}
\begin{equation}h_t=r_t\bigodot g(c_t)+(1-r_t)\bigodot s_t\end{equation}
可以看出其相较于之前的模型最大的差别在于门转态不再和之前转态有关
这意味着什么?
意味着 我们不再需要等着迭代
在预处理的时候 就可以把所有门状态值计算出来
!!!而且这些门的计算都是复杂度十分高的矩阵乘法
注意这里的是矩阵乘法 而下面隐层$h_t$中的运算都是矩阵的Hadamard乘--对应$i,j$直接相乘
这两者的复杂度差别十分大了
所以 SRU这类模型 最大的贡献就是 提升 RNN运算速度
当然 SRU 并没有不依赖前者转态
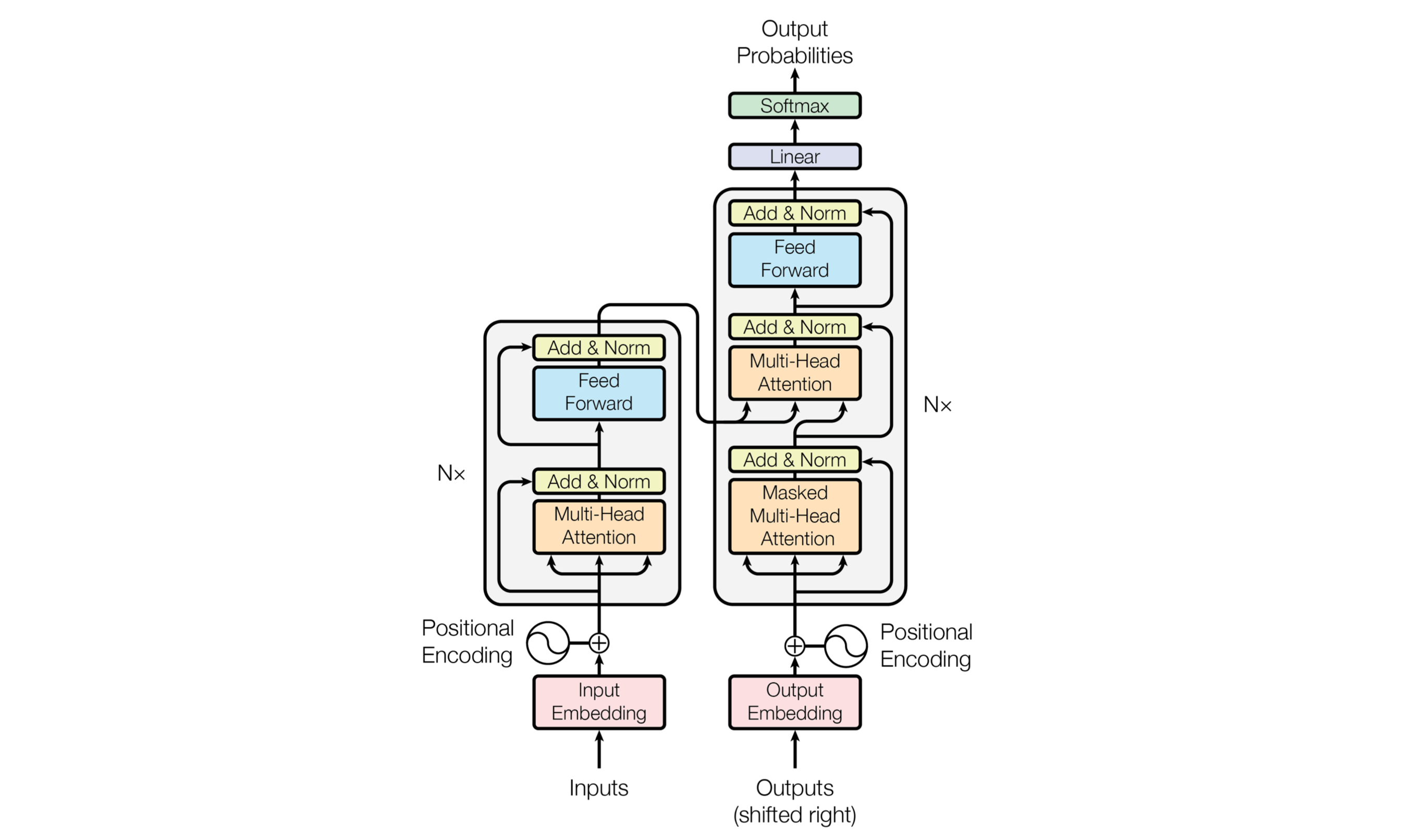
self-attention
当然 dalao 也不会闲着
就在大家已经觉得时序就=RNN的时候
Google Brain的 dalao 发了一篇题目就很拉风的 paper
简单来说 其一次性计算出带较长语句的word encodeing
通过 positional matrix 来获得时序信息
这样的好处就是可以并行计算 在计算性能上较 RNN 更优
self-attention 的另外一个优点就是寻找时序关系更优
尤其是适合在跳跃 topic 的语料中
举个例子聊天聊到一半你说你去收个衣服,在这里 topic 就中断了,直到你再次回来
position 的方式更容易计算之间的关系 而不用担心梯度消失
- 具体公式
\begin{equation}\text{Attention}(Q,K,V) =\text{softmax}(\dfrac{QK^T}{\sqrt{d_k}})V\end{equation}
\begin{equation}Q\in R^{n\times d_k},K\in R^{d_k\times m},V\in R^{m\times d_v}\end{equation}
\begin{equation}\text{Attention}(q_t,K,V) =\sum\limits_{s=1}^m\dfrac{1}{z}exp(\dfrac{<q_t,k_s>}{\sqrt{d_k}})v_s\end{equation}
\begin{equation}\text{head}_i = \text{Attention}(QW_i^Q,KW_i^K,VW_i^V)\end{equation}
\begin{equation}\text{MultiHead}(Q,K,V) = \text{concat}(\text{head}_1, \text{head}_2,...,\text{head}_h)\end{equation}
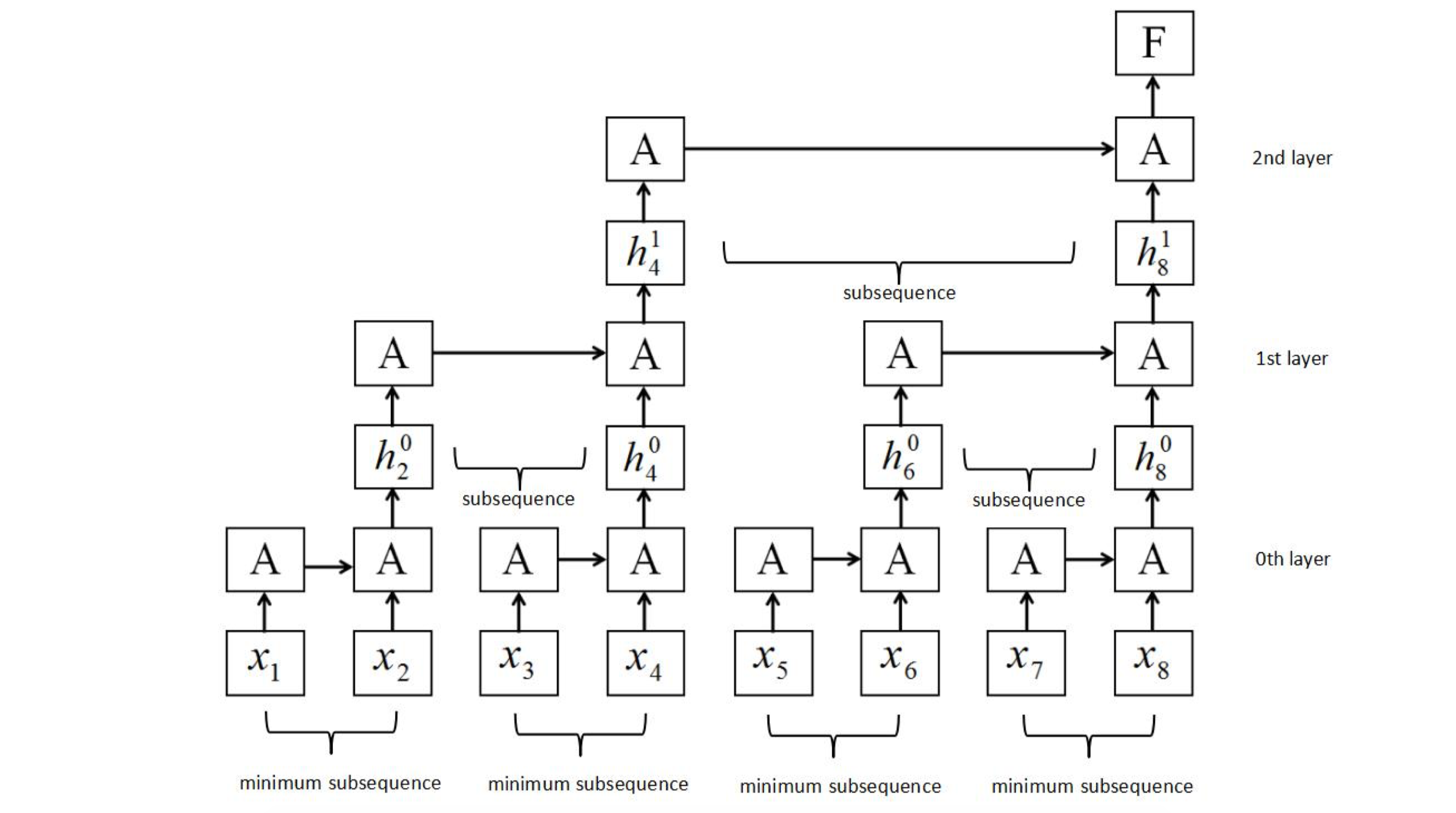
Sliced Recurrent Neural Networks
从上文我们可以知道 RNN 的结构是链式的
必须在前者进行完之后才能进行下一步
通过类似二分的思想对 RNN 运行顺序进行优化 也得到了较好的结果
然后[6]中周志华 dalao 利用 FSA 对 RNN 过程进行捕捉 从而进行可解释分析
Reference
- Understanding LSTM Networks
- The Unreasonable Effectiveness of Recurrent Neural Networks
- 如何评价新提出的 RNN 变种 SRU?
- LONG SHORT-TERM MEMORY
- Supervised Sequence Labelling with Recurrent Neural Networks
- Learning with Interpretable Structure from RNN
- Sliced Recurrent Neural Networks
- Simple Recurrent Units for Highly Parallelizable Recurrence
- Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling
- Attention Is All You Need